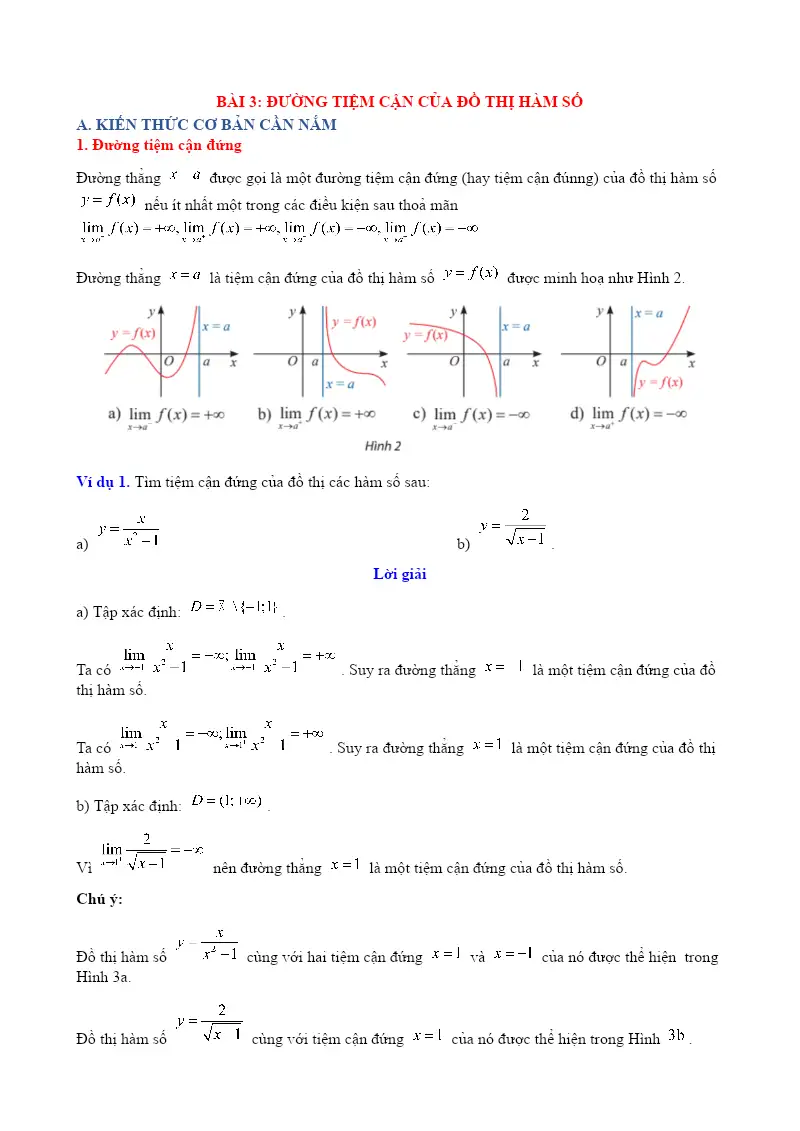
BÀI 3: ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ A. KIẾN THỨC CƠ BẢN CẦN NẮM 1. Đường tiệm cận đứng Đường thẳng xa được gọi là một đurờng tiệm cận đứng (hay tiệm cận đúnng) của đồ thị hàm số ()yfx nếu ít nhất một trong các điều kiện sau thoả mãn lim(),lim(),lim(),lim() xaxaxaxa fxfxfxfx    Đường thẳng xa là tiệm cận đứng của đồ thị hàm số ()yfx được minh hoạ như Hình 2. Ví dụ 1. Tìm tiệm cận đứng của đồ thị các hàm số sau: a) 21 x y x  b) 2 1y x  . Lời giải a) Tập xác định: \{1;1}Dℝ . Ta có 2211lim;lim 11xx xx xx  . Suy ra đường thẳng 1x là một tiệm cận đứng của đồ thị hàm số. Ta có 2211lim;lim 11xx xx xx  . Suy ra đường thẳng 1x là một tiệm cận đứng của đồ thị hàm số. b) Tập xác định: (1;)D . Vì 1 2 lim 1xx  nên đường thẳng 1x là một tiệm cận đứng của đồ thị hàm số. Chú ý: Đồ thị hàm số 21 x y x  cùng với hai tiệm cận đứng 1x và 1x của nó được thể hiện trong Hình 3a. Đồ thị hàm số 2 1y x  cùng với tiệm cận đứng 1x của nó được thể hiện trong Hình 3 b .